Flowers, Staircases and The Golden Ratio

An Unusual Counting Problem

Have you ever climbed a staircase that just didn’t seem to be made for human legs?

The steps are too small to comfortably take one at a time, but too large for an easy double-stair.

You either end up shuffling along with baby-steps, or stretching so far that it feels like you’re trying out for the gymnastics team.

In situations like these, you might start to wonder (or maybe it’s just me?): how many different ways could you actually climb this staircase, taking just one or two stairs at a time?

---

Suppose there’s just 10 steps in our staircase.

We could climb the steps in the following sequences of moves:

1 1 1 1 1 1 1 1 1 1, n

2 1 1 1 1 1 1 1 1,

1 2 1 1 1 1 1 1 1,

1 1 2 1 1 1 1 1 1,

1 1 1 2 1 1 1 1 1,

1 1 1 1 2 1 1 1 1,

⋮

1 1 2 2 2 2,

2 2 2 2 2,

There’s clearly going to be a lot of options to count, so maybe listing them all out isn’t the best idea.

---

Let’s try a different approach. 

We can denote the number of ways to climb exactly n stairs as xₙ. 

When we reach the nth stair, our previous move must have been either of size 1 or size 2. Therefore, we must have just been on step n-1 or n-2

There’s only 1 way to get from step n-1 to step n in one go, and similarly, there’s only 1 way to get from step n-2 to step n in one go. 

Therefore, the number of ways to reach step n is the same as the number of ways to reach step n-1 plus the number of ways to reach step n-2. This gives us the recurrence relation

xₙ = xₙ₋₁ + xₙ₋₂

…where xₙ₋₁ and xₙ₋₂ are the number of ways we could have reached steps n-1 and n-2 respectively.

We can repeat this argument even further. If we were on step n-1 then, one move before that, we must have been on either step n-2 or n-3. 

Therefore the number of ways we can reach the nth stair can be defined recursively. This means that we calculate it in terms of the number of ways we can reach the steps before it.

---

Let’s take a look at some simple cases and build our way up.

For n=0, there’s exactly 1 way to climb zero stairs, that is, by doing nothing at all.

For n=1, there is obviously only one way that we can reach the first stair.

For n=2, there are 2 ways we can reach it: either two moves of size 1, or one move of size 2.

x₀ = 1

x₁ = 1

x₂ = 2

Using the recurrence relation we defined above, we have that:

Hence there are 89 different ways we can reach the 10th stair, climbing either one or two steps at a time.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

This sequence may look familiar; it’s one of the most famous sequences in mathematics, and it’s known as the Fibonacci sequence.

It has many applications such as in computer science, architecture and design, and is even used by traders to make predictions about the stock market. The Fibonacci sequence also pops up in many unexpected places in nature.

For example many flowers have a Fibonacci Number of petals (a number that appears in the Fibonacci sequence).

• Buttercups have 5 petals
• Marigolds have 13 petals
• Daisies often have 34 or 55 petals
• The head of a sunflower has seeds in a spiral shape. If you count the number of arms in those spirals, you will find a Fibonacci number. It doesn’t matter if you count them going clockwise or anticlockwise, in fact, they will both work and give you two different Fibonacci numbers!

*Disclaimer. To avoid disappointing anyone who just ventured out to the garden to start counting flowers, please be warned that the exact number of petals may vary, and many selectively bred plants may have a different number of petals. Or one could just have fallen off.

The Golden Ratio

The ratio of pairs of consecutive terms in the sequence approaches a value known as the Golden Ratio. This is often represented using the Greek letter Phi, φ.

3/2 = 1.5 

5/3 = 1.667 

8/5 = 1.6 

13/8 = 1.625 

21/13 = 1.615 

34/21 = 1.619 

φ ≈ 1.618033988

Phi is an irrational number, and has an exact value given by:

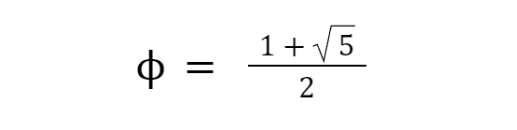
We can use this value to give us a shortcut to solving the staircase problem.

The number of ways to get to the nth stair is given by Binet’s Formula:

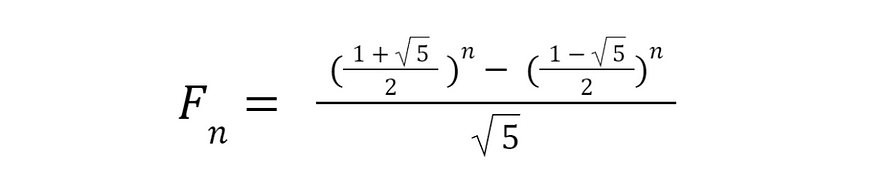
It may look a little complicated, a calculator can easily do the heavy lifting here.

---

It’s worth pointing out that the Fibonacci sequence starts with the first term, F₀ = 0

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … 

whereas our sequence starts with the first term x₀ = 1

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Meaning that our solution sequence is offset by 1. Therefore, for this situation, we actually require F₁₁ to give us the number of ways to reach the 10th stair.

*We could extend our sequence by saying that there are zero ways to climb -1 stairs since it’s not possible to have -1 stairs (at least as far as I know). 
We could then neatly shift each element along one position so everything matches up.

---

Let’s see if we get the same answer as before:

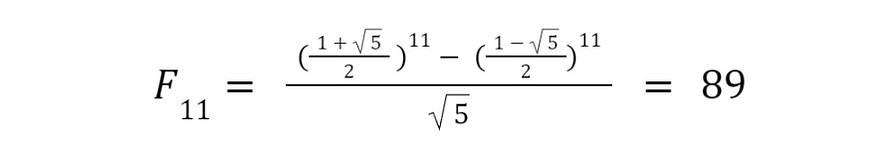
Amazingly, when we substitute n=11 into this formula, it spits out a nice round number, and exactly the same as we worked out before.

Using this formula, it’s easy to work out a solution for any number of steps.

If we increase the size of the problem to 100 stairs (again doing either 1 or two steps at a time) then there are exactly 573147844013817084101 combinations of ways we can walk up them.

With 1000 steps the number of combinations becomes astronomical:

70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501

That’s a lot of walking up and down stairs!

---

Thanks for reading 🙂

*Unless otherwise stated, all images are by the author.