Surviving the First Year of Your Math Degree
Everything I Wish I’d Known Before Studying Mathematics at University

Luckily, studying for a degree in mathematics is different from high school.
Math class didn’t exactly get the best reputation in school — and I can see why. It tells students to learn about seemingly pointless techniques and memorise different formulas that 99% of them will never use again — unless they go on to become math teachers.
Things change, however, when you decide to study maths at a higher level.
Mathematics becomes much more precise, and more transparent, and emphasises problem-solving over performing the same laborious calculations you’ve done hundreds of times before from a textbook.
It becomes a transferrable skill that you can build and develop and will serve you in many different areas of work. You also start studying more advanced concepts that are useful in engineering, economics, computer science, or pretty much any STEM subject.
But it’s also a big adjustment, and if you don’t know what you’re getting in for, it can be quite a shock. So here’s a list of things I wish I’d known before arriving at my first lecture.
Language
The first thing you will notice when picking up a math textbook or paper is the language the author uses.
These books are filled with strange, complicated-looking symbols and long, complicated-sounding sentences that don’t seem to get to the point and give way too much unnecessary detail. This is on purpose.
Studying mathematics is about precision. We need to be precise when we are talking about an idea so that we are absolutely clear about what we mean, and about what we don’t mean.
The sentences may sound long-winded, but there are often a lot of clauses and clarifications to make sure we all have the same understanding.
If, for example, we wanted to choose a number between 1 and 10,
A normal person might say something like:
“Choose a number between 1 and 10”.
Is this simple and easy to understand for the average person? …yes.
Is it mathematically precise? …no.
Should we include 1 and 10 themselves? Should we include fractions, what about pi, can we choose that as our number?
A rigorous mathematical statement leaves no room for follow-up questions. Instead, a mathematician would say something like:
“Let n∈ℕ such that 1 ≤ n < 10”
Granted, if you don’t understand the symbols, this may not be so easy to decipher, but once you get a handle on the notation, this statement is clear, precise, and only has one meaning. Let’s break it down.
“Let n∈ℕ” means that we choose a number from the set of natural numbers (the positive integers not including zero) and henceforth refer to this number as n. We choose this number so that it satisfies the following condition: “1 ≤ n < 10”, so our number must be between 1 and 9 inclusive.
See how this is a much more long-winded way of phrasing it?
Mathematicians also enjoy naming things that they create, so rather than just choosing a number, they’ll choose it, and then give it a name (in this case n) so that they can easily refer to it later on.
Notation
Often in mathematics, we use letters to name objects that we create. For example, we might choose a number, n, or a sequence of numbers: n₁, n₂, …, nₖ. This indicates that we choose k numbers and refer to each of them by name. The subscript next to the n refers to the position in the sequence.
We might then choose an arbitrary element from this sequence that we would refer to as nᵢ, since i is just an arbitrary number.
We also make use of set notation.
A set is just an unordered collection of objects where there are no duplicates. We denote the list of elements of a set using { }.
We can either list the elements explicitly:
{1, 2, 3, 4}
use ellipses to indicate a range of values:
{1, 2, 3, …, n-1, n}
or we can use some expression to indicate what numbers go into our set:
S = {x∈ℤ | x² + 2x > 394}
(Here, we create a set and name it S)
To choose an arbitrary element from a set, or to indicate that an element belongs to a set, we use the symbol: ∈, which loosely translates to “in” or “element of”. So n∈S would indicate that we choose an element that is in S.
We also see the symbols: ⇒ and ⇔. The single arrow, ⇒, is used to mean ‘implies’. So statement A implies statement B or A⇒B. This is the same as saying: If A is true then B is true. (if … then…).
You may also see this arrow written back to front:
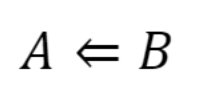
to mean B implies A or A is implied by B. Sometimes it is easier to write this than to put B⇒A.
It’s important to point out a subtlety here:
A⇒B means that if A is true then B is true.
This does not necessarily mean that since B is true, A must also be true. You cannot reverse the statement.
However, sometimes you will see ⇔. This means that A⇒B and B⇒A. So A implies B and B implies A.
In this case, we would say that statements A and B are equivalent. One statement is true when the other is true, and only when the other is true. Both statements are either true or false. You cannot have one true and one false.
This is sometimes phrased as A is true if and only if B is true.
Structure
Perhaps the most obvious difference between a high school and a degree-level math textbook is its structure. Most Textbooks and papers all follow the same format:
Definitions → Theorem → Proof
Definitions define keywords and mathematical objects that we are then allowed to use. Most of the time, if we haven’t defined something, it would be improper to start performing calculations with it. In a similar vein, we can’t perform an operation on something if we aren’t clear about exactly what that operation does and when it can be used. This goes for variables within a definition too. It would be imprecise to say:
“p is a prime if its only factors are 1 and itself”
What is this p thing that we are calling a ‘prime’? Where does it come from? What values is it allowed to take? Is it even a number — could it be a matrix, set, or function?
A much better definition would be:
Let p be a positive integer greater than 1. We say that p is a prime if the only positive integers that divide it are 1 and p itself.
We now know where this p thing comes from, and what type of values it can take. If we’re being pedantic, we should also really define what we mean by “divides” but let’s assume that’s already been covered.
Again, this is all done for clarity; we need to make sure we all have precisely the same understanding of what we’re talking about.
Once we have constructed a few definitions, we start looking at propositions and theorems. These are just mathematical facts about definitions we’ve just established.
A theorem is a really important result that has consequences for many other ideas in mathematics. Think Pythagoras’ Theorem.
A proposition is similar except it’s just less important. It will still have applications, it’s just perhaps not as ground-breaking as a theorem.
A proposition or theorem that is claimed to be true is known as a conjecture. It is only called a proposition or theorem once it has been proven to be correct.
A proof is a mathematical argument. You need to be careful here and ensure that there is no error in each step of your argument. If you make a mistake, you could accidentally prove something that is not actually true.
Oftentimes, it will be clear if a statement is supposed to be true or not so you probably won’t start breaking the foundations of mathematics.
The more likely scenario is that you make an invalid step in a proof and draw some conclusion that you’re not allowed to do. This won’t completely invalidate your proof, but you’ll probably get some feedback saying:
“yes, but why?”
Oftentimes, the answer you give will be correct, but your justification as to why it is correct is insufficient.
For a lot of proofs, the most difficult part is knowing where to start. Once you get going, things often fall nicely into place.
After we have proven a theorem, there may then be some other simple theorems that you can determine to be true as a direct consequence. This is known as a corollary.
And that’s pretty much it. This structure is just repeated over and over again. Define keywords and objects, claim that some facts about them are true, then prove that they are indeed true and that it isn’t just some wild accusation. After that, we might go and do some calculations using the result of these theorems, or build a new method or algorithm for something.
As an example, we might start by playing around with different types of equations and notice a pattern with equations containing an x² term. We call these equations quadratics and give a formal definition so we know exactly what is and isn’t part of this category of equations. Then we start trying to solve these equations and eventually come up with a formula that we think might give us a solution to any quadratic equation. This is exciting as it would make solving them much easier, but we still need to prove it.
We write it out precisely as a theorem so that we know what each part of the formula means and what type of equations we are attempting to solve with it. We then attempt to prove the theorem and find it to be true.
Next, we notice that the formula only gives nice solutions when one of the terms is zero or positive, so we write this fact out as a proposition and then prove it. We find this to be true as well.
With all of these definitions and theorems in place, we now start using the formula that we came up with to solve some of these equations.
Congratulations, you’ve just invented the quadratic formula!
This is what the study of mathematics is really about: we invent some hypothesis, explore the idea, test it, prove it is right or wrong, and then apply it to solve some problem.
Throughout school, students only focus on the last part of this: the ‘doing something’ part, but there’s a whole other side of mathematics that most people never get to see.
The real skill of mathematics is in being precise and accurate with language; thinking critically and creatively to generate ideas for proofs; understanding complex and abstract ideas, and having the ability to construct a valid, logical argument.
That’s why we study mathematics.
And you’re in for a treat.

