The Tower of Hanoi
The Math Behind The Classic Puzzle

You’ve probably seen this puzzle before.
You could probably solve it without too much hassle.
But let’s ask a more interesting question…
What is the fewest number of moves required to solve the puzzle?
Can we prove we’re correct?
First, let’s make sure we’re all on the same page, for the benefit of those who haven’t seen this problem before.
We start with a board with 3 vertical pegs sticking out of it. There are 5 rings stacked on the left-most peg as shown in the image below. The goal is to move the stack of rings from the left peg to the right peg.
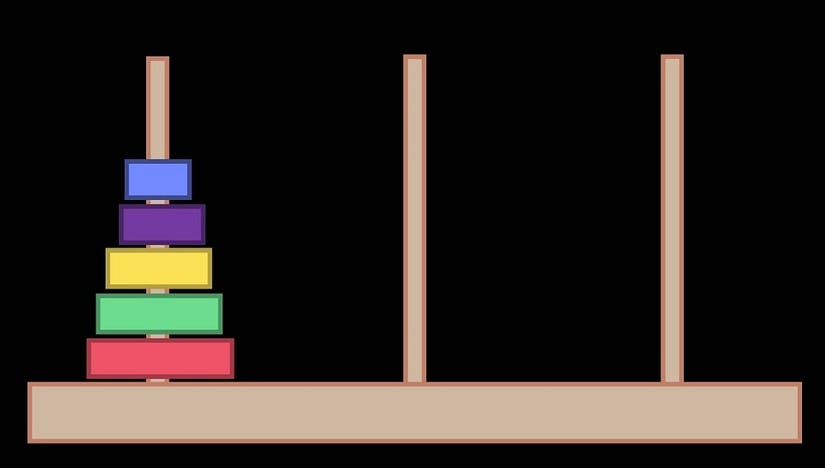
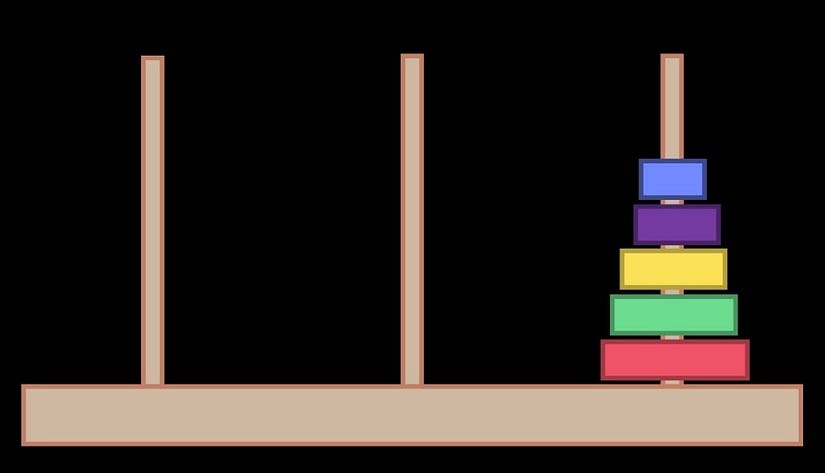
But there are a few rules:
- You can only move one ring at a time,
- You can only move the top ring from a peg,
- You cannot put a larger ring on top of a smaller one.
We can increase the complexity of this puzzle by increasing the number of rings, but the number of pegs always stays the same
You can find an online version of this puzzle here if you want to try it out.
After a couple of attempts, you’ll probably be able to solve it in the least possible moves and do so relatively quickly. It takes a little longer when you add more rings, but the principle remains the same.
But where does this optimal number come from?
Let’s look at a simpler example. What if there was just one ring?
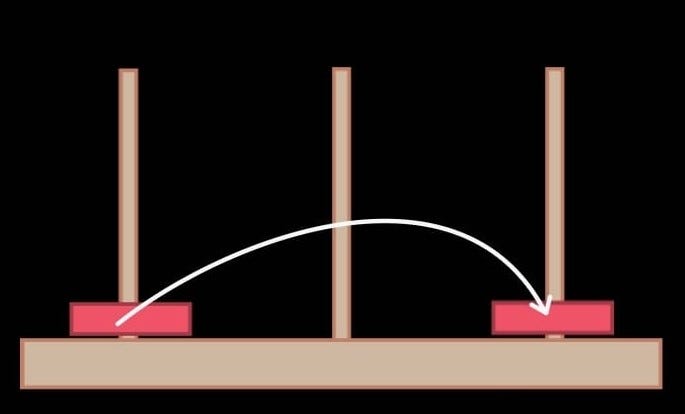
This is not a trick question: it takes just one move to solve the puzzle, and obviously, this number is optimal.
What about with 2 rings?
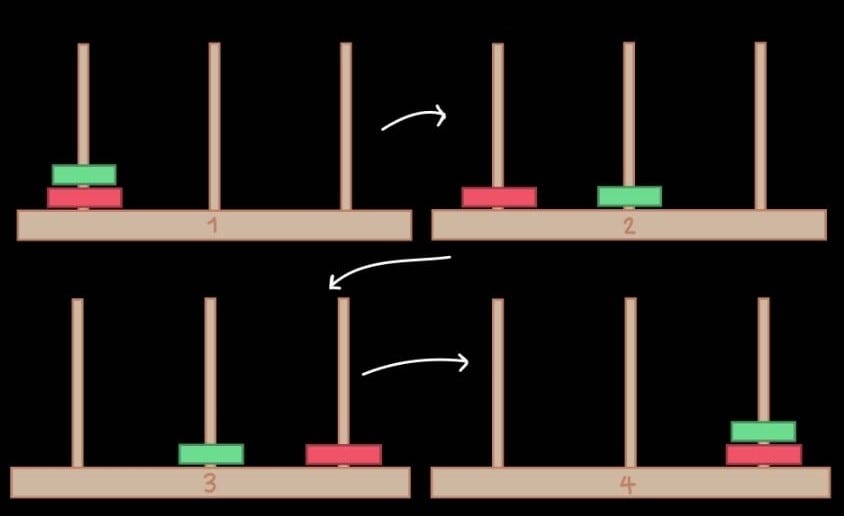
Then 3 moves are required to solve it. Again, this number is optimal.
It takes a little more time to calculate the answer for 3 rings, but you should end up with a minimum total of 7 moves.
It turns out that for 4, 5, and 6 rings the optimal number of moves is 15, 31, and 63.
If you know your powers of 2, then you might start to notice a pattern here…
Claim: Let Hₙ be the number of moves required to solve the Tower of Hanoi puzzle with n rings. Then:
Hₙ = 2ⁿ -1
Before we try to prove this claim, let’s look at the strategy we employ for an optimal solution.
Take a look at these four states from the optimal solution when we have 5 rings (n=5)
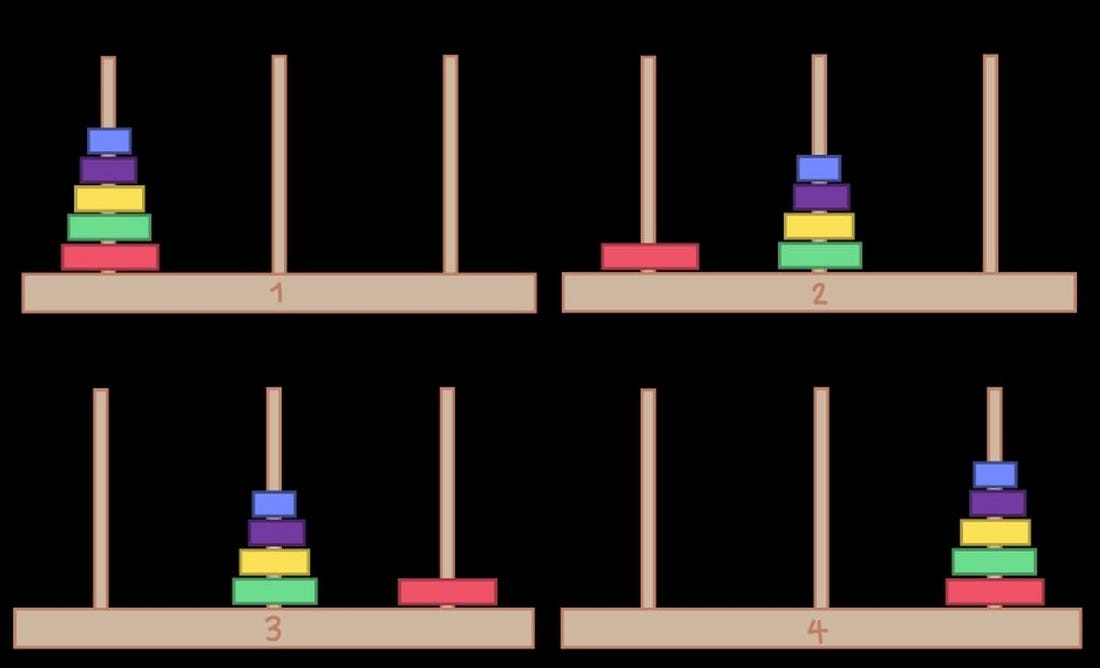
We can break down the solution into 3 steps.
- Move the top n-1 rings to the middle peg
- Move the bottom ring to the right
- Move the n-1 rings to the right peg
But how many moves do we need to complete each step?
The second step is the easiest to work out; it takes just one move.
The first step requires us to move n-1 rings from one peg to another. This is just like if we had solved the entire puzzle but with 4 rings instead of 5.
If we call the optimal number of moves Hₙ, then step 1 requires Hₙ₋₁ moves (the number of moves required for n-1 rings).
It’s the same for step 3 as well, since we are moving n-1 rings from one peg to another.
Using this idea, we can form an equation.
Hₙ = Hₙ₋₁ + 1 + Hₙ₋₁
Or more simply:
Hₙ = 2*Hₙ₋₁ + 1
Let’s see how we can use this equation to help us prove our formula is correct.
We’ll prove this formula using a technique known as proof by induction.
The idea is to prove that if the formula is true for some arbitrary number (k) then it is also true for (k+1)
Then, if we know that it’s true for k=1, it must also be true for the next number, k=2.
If it’s true for k=2 then it must also be true for the next number, k=3.
If it’s true for k=3, then it must also be true for the next number, k=4,
And so on…
This argument can be repeated again and again until infinity. So the formula must be true for all possible values of n.
Let’s get started with the proof.
Claim: Let Hₙ be the number of moves required to solve the Tower of Hanoi puzzle with n rings. Then:
Hₙ = 2ⁿ -1
Proof.
We start by proving the formula works for n=1.
H₁ = 2¹-1 = 1
and the smallest number of moves for a single ring is 1. Checks out so far.
Now let’s assume that the formula works for an arbitrary number, k. Therefore, we are assuming that:
Hₖ = 2ᵏ -1
Now for the tricky step. We now want to show that if it’s true for k, then it’s also true for k+1.
Using the equation we found earlier, we know that
Hₖ₊₁ = 2*(Hₖ) +1
Therefore
Hₖ₊₁ = 2*(2ᵏ -1) +1
using the assumption we just made. So then
Hₖ₊₁ = 2*2ᵏ — 2 + 1
Hₖ₊₁ = 2ᵏ⁺¹ -1
Which looks like our formula, except we have k+1 instead of k. So the formula is true for k+1 if it is true for k.
And that’s all the heavy lifting done.
We’ve shown that the formula is correct when k=1. We’ve shown that if it’s true for some value then it’s true for the next value. So this statement must be true for 2, 3, 4, 5, … and so on.
Using this formula, we find that a puzzle with 10 rings would require at least 1023 moves, and a puzzle with 25 rings would need at least 33554431.
That sounds like a lot, but if you perform one move every second, it would take 388 days, 8 hours, 40 mins, and 31 seconds to finish the puzzle. Now it really sounds like a lot.
While the Tower of Hanoi might seem straightforward at first glance, there’s far more to it than meets the eye. It’s easy to underestimate its complexity, but the puzzle introduces some fascinating concepts worth exploring.
Beyond the challenge itself, it serves as a great gateway into the world of mathematical proof and highlights the intricacies of counting problems, an area of study known as combinatorics.
Whether you’re a puzzle enthusiast or a budding mathematician, the Tower of Hanoi offers an engaging challenge and a deeper understanding of problem-solving techniques.
Thanks for reading 🙂
*Unless otherwise stated, all images are by the author.

